16.7. Группы точек
16.7.1. Группы точек эллиптических кривых
Эллиптическая кривая $E$ над полем вещественных чисел записывается в виде уравнения, связывающего координаты $x$ и $y$ точек кривой:
где $a,b \in {{\mathbb{R}}}$ – вещественные числа. Эта форма представления эллиптической кривой называется формой Вейерштрасса.
На кривой определён инвариант:
Пусть $x_{1}$, $x_{2}$ и $x_{3}$ – корни уравнения $x^3 + a x + b = 0$. Определим дискриминант $D$ в виде:
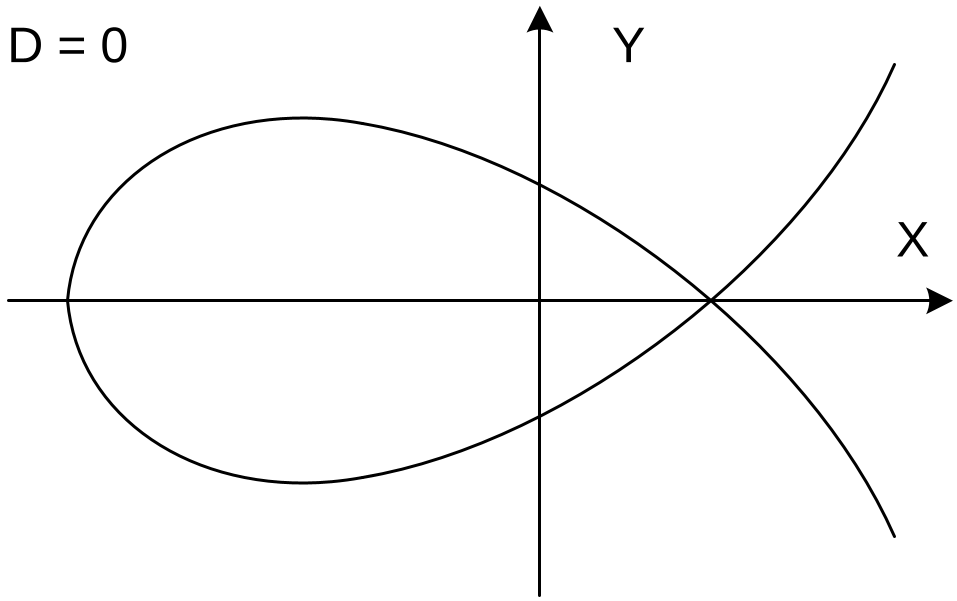
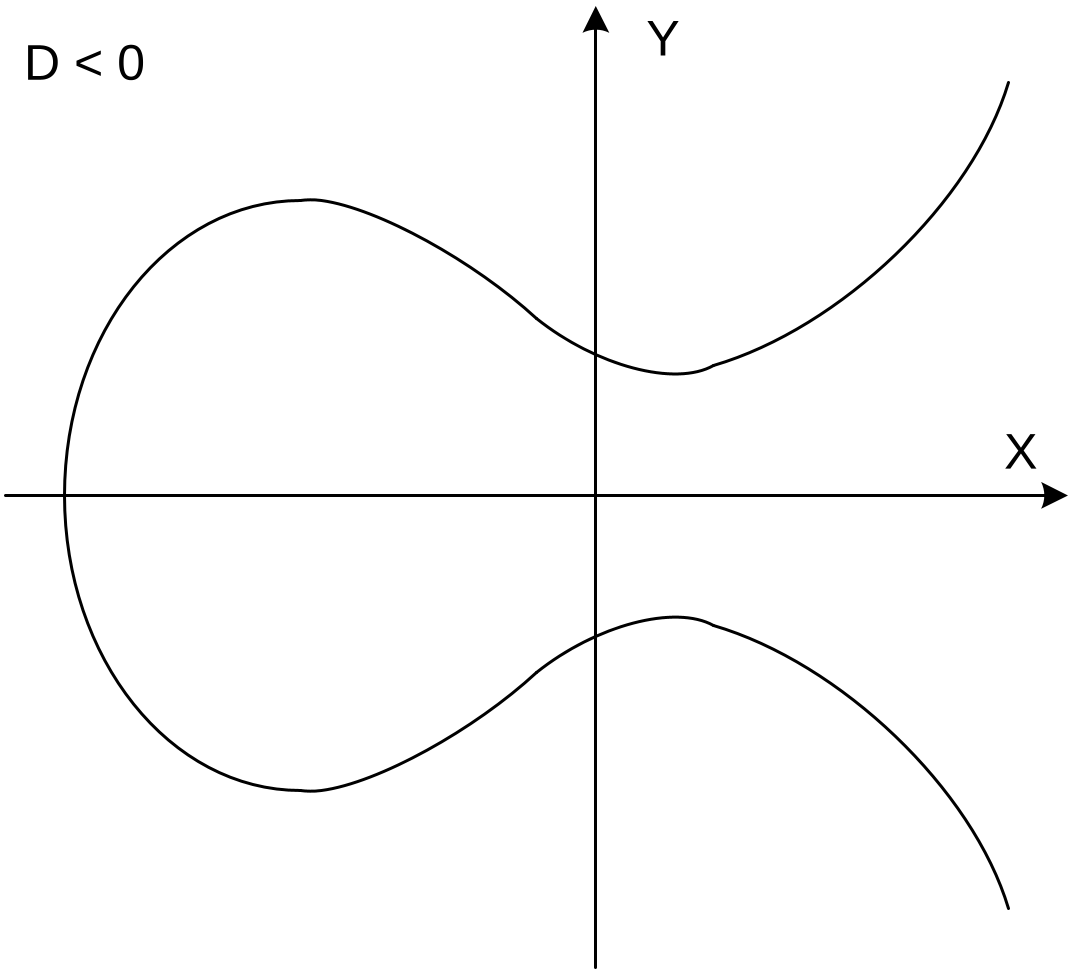
Рассмотрим различные значения дискриминанта $D$ и соответствующие им кривые, которые представлены на рисунках 16.1a, 16.1b, 16.1c.
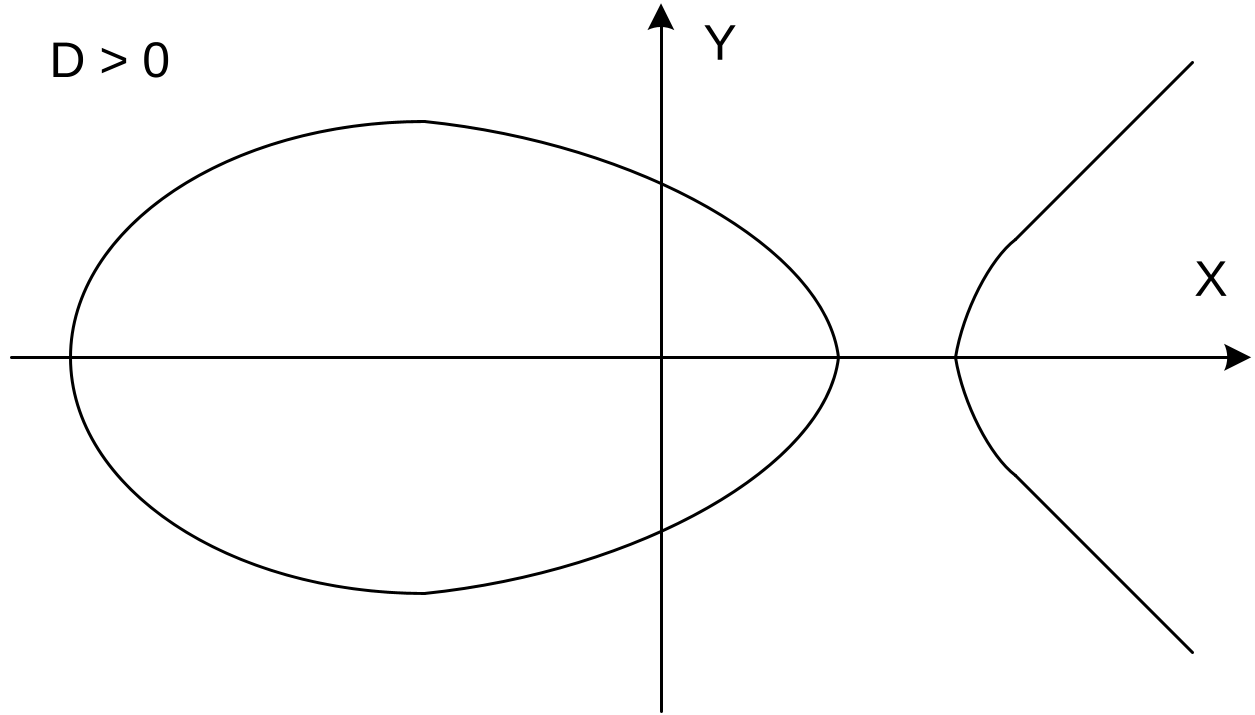
- При $D>0$ график эллиптической кривой состоит из двух частей (см. рис. 16.1a). Прямая, проходящая через точки $P(x_1; y_1)$ и $Q(x_2; y_2)$, обязательно пересечёт вторую часть кривой в точке с координатами $(x_3; \widetilde{y}_3)$, отображением которой является точка $R(x_3; y_3)$, где $y_3 = - \widetilde{y}_3$. Любые точки на кривой при $D>0$ являются элементами группы по сложению.
- Если $D=0$, то левая и правая части касаются в одной точке (см. рис. 16.1b). Эти кривые называются сингулярными и не рассматриваются.
- Если $D<0$, то записанное выше уравнение [Wer] описывает одну кривую, представленную на рис. 16.1c.
Рассмотрим операцию сложения точек на эллиптической кривой при $D \ne 0$ (другие кривые не рассматриваются).
Пусть точки $P(x_1; y_1)$ и $Q(x_2; y_2)$ принадлежат эллиптической кривой (рис. 16.1a). Определим операцию сложения точек
- Eсли $P \neq Q$, то точка $R$ определяется как отображение (инвертированная $y$-координата) точки, полученной пересечением эллиптической кривой и прямой $PQ$. Совместно решая уравнения кривой и прямой, можно найти координаты их точки пересечения. Зная координаты точки пересечения, можно вычислить и координаты искомой точки $R = (x_3; y_3)$, которые будут равны:
$$ x_3 = \lambda^2 - x_1 - x_2, $$$$ y_3 = - y_1 + \lambda (x_1 - x_3), $$где$$ \lambda = \frac{y_2 - y_1}{x_2 - x_1} $$есть тангенс угла наклона между прямой, проходящей через точки $P$ и $Q$, и осью $x$. Теперь рассмотрим специальные случаи.
- Пусть точки совпадают: $P = Q$. Прямая $PQ$ превращается в касательную к кривой в точке $P$. Находим пересечение касательной с кривой, инвертируем $y$-координату полученной точки, это будет точка $P + P = R$. Тогда $\lambda$ – тангенс угла между касательной, проведённой к эллиптической кривой в точке $P$, и осью $x$. Запишем уравнение касательной к эллиптической кривой в точке $(x; y)$ в виде:
$$ 2 y y' = 3 x^2 + a. $$Производная равна$$ y' = \frac{3 x^2 + a}{2 y}, $$и$$ \lambda = \frac{3 x_1^2 + a}{2 y_1}. $$Координаты $R$ имеют прежний вид:$$ x_3 = \lambda^2 - x_1 - x_2, $$$$ y_3 = - y_1 + \lambda (x_1 - x_3), $$
- Пусть $P$ и $Q$ – противоположные точки, то есть $P=(x; y)$ и $Q=(x; -y)$. Введём ещё одну точку на бесконечности и обозначим её $O$ (точка $O$ или точка 0 «ноль», или альтернативное обозначение $\infty$). Результатом сложения двух противоположных точек определим точку $O$. Точка $Q$ в данном случае обозначается как $-P$:
$$ P = (x; y), ~ -P = (x; -y), ~ P + (-P) = O. $$
- Пусть $P = (x; 0)$ лежит на оси $x$, тогда
$$ -P = P, ~ P + P = O. $$
Все точки эллиптической кривой, а также точка $O$ образуют коммутативную группу ${{\mathbb{E}}}({{\mathbb{R}}})$ относительно введённой операции сложения, то есть выполняются законы коммутативной группы:
- сумма точек $P + Q$ лежит на эллиптической кривой;
- существует нулевой элемент – это точка $O$ на бесконечности:
$$ \forall P \in {{\mathbb{E}}}({{\mathbb{R}}}): ~ O + P = P; $$
- для любой точки $P$ существует единственный обратный элемент $-P$:
$$ P + (-P) = O; $$
- выполняется ассоциативный закон:
$$ (P + Q) + F = P + (Q + F) = P + Q + F; $$
- выполняется коммутативный закон:
$$ P + Q = Q + P. $$
Сложение точки с самой собой $d$ раз обозначим как умножение точки на число $d$:
16.7.2. Эллиптические кривые над конечным полем
Эллиптические кривые можно строить не только над полем рациональных чисел, но и над другими полями. То есть координатами точек могут выступать не только числа, принадлежащие полю рациональных чисел ${{\mathbb{R}}}$, но и элементы поля комплексных чисел $\mathbb{C}$ или конечного поля ${{\mathbb{F}}}$. В криптографии нашли своё применение эллиптические кривые именно над конечными полями.
Далее будем рассматривать эллиптические кривые над конечным полем, являющимся кольцом вычетов по модулю нечётного простого числа $p$ (дискриминант не равен 0):
Возможна также более компактная запись:
Точкой эллиптической кривой является пара чисел
удовлетворяющая уравнению эллиптической кривой, определённой над конечным полем ${{\mathbb{Z}}}_p$.
Операцию сложения двух точек $P = (x_1; y_1)$ и $Q = (x_2; y_2)$ определим точно так же, как и в случае кривой над полем вещественных чисел, описанном выше.
- Две точки $P = (x_1; y_1)$ и $Q = (x_2; y_2)$ эллиптической кривой, определённой над конечным полем ${{\mathbb{Z}}}_p$, складываются по правилу:
$$ P + Q = R \equiv (x_3; y_3), $$$$ \begin{cases} x_3 = \lambda^2 - x_1 - x_2 \mod p,\\ y_3 = - y_1 + \lambda (x_1 - x_3) \mod p,\\ \end{cases} $$где$$ \lambda = \begin{cases} \dfrac{y_2 - y_1}{x_2 - x_1} \mod p, & \text{ если } P \ne Q, \\ \\ \dfrac{3 x_1^2 + a}{2 y_1} \mod p, & \text{ если } P = Q. \\ \end{cases} $$
- Сложение точки $P=(x; y)$ c противоположной
$(-P) = (x; -y)$ даёт точку в бесконечности $O$: gather* P + (-P) = O, (x_1; y_1) + (x_1; -y_1) = O, (x_1; 0) + (x_1; 0) = O.
Мы рассматриваем эллиптические кривые над конечным полем ${{\mathbb{Z}}}_p$, где $p > 3$ – простое число, элементы ${{\mathbb{Z}}}_p$ – целые числа $\{0, 1, 2, \ldots, p-1\}$, то есть исследуем следующее уравнение двух переменных $x, y \in {{\mathbb{Z}}}_p$:
где $a, b \in {{\mathbb{Z}}}_p$ – некоторые константы.
Как и в случае выше, множество точек над конечным полем ${{\mathbb{Z}}}_p$, удовлетворяющих уравнению эллиптической кривой, вместе с точкой в бесконечности $O$ образуют конечную группу ${{\mathbb{E}}}({{\mathbb{Z}}}_p)$ относительно описанного закона сложения:
По теореме Хассе порядок группы точек $|{{\mathbb{E}}}({{\mathbb{Z}}}_p)|$ оценивается как
или, в другой записи,
16.7.3. Примеры группы точек
Пример 1
Пусть эллиптическая кривая задана уравнением
Найдём все решения этого уравнения, а также количество точек $|{{\mathbb{E}}}({{\mathbb{Z}}}_p)|$ на этой эллиптической кривой. Для нахождения решений уравнения составим следующую таблицу:
| $x$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| $y^2$ | 1 | 2 | 2 | 0 | 2 | 0 | 0 |
| $y_1$ | 1 | 3 | 3 | 0 | 3 | 0 | 0 |
| $y_2 = - y_1 \mod p$ | 6 | 4 | 4 | 4 |
Выпишем все точки, принадлежащие данной эллиптической кривой ${{\mathbb{E}}}({{\mathbb{Z}}}_p)$:
Получили
Проверим выполнение неравенства Хассе:
Следовательно, неравенство Хассе выполняется.
Минимальное натуральное число $s$ такое, что
будем называть порядком точки $P$.
Пример 2
Группа точек эллиптической кривой
состоит из точек:
Порядок группы:
Порядок группы точек по теореме Хассе:
Порядки возможных подгрупп: 2, 3, 4, 6 (все возможные делители порядка группы 12).
Найдём порядок точки $A = (-8; 7)$. Так как возможные порядки подгрупп (и всех точек группы) известны, нужно проверить только их.
- $2A = A + A = (-5; 3)$:
$$\begin{aligned} & R = P + P, P = (-8; 7), \\ & \lambda = \frac{3 x_P^2 + a}{2y_P} = \frac{3 \cdot (-8)^2 + 5}{2 \cdot 7} = 8 \mod 17, \\ & x_R = \lambda^2 - 2x_P = 8^2 - 2 \cdot (-8) = -5 \mod 17, \\ & y_R = \lambda (x_P - x_R) - y_P = 8 \cdot ((-8) - (-5)) - 7 = 3 \mod 17, \\ & R = (-5; 3). \\ \end{aligned}$$
- $3A = 2A + A = (-6; 7)$:
$$\begin{aligned} & R = P + Q, P = (-8; 7), Q = (-5; 3), \\ & \lambda = \frac{y_Q - y_P}{x_Q - x_P} = \frac{3 - 7}{-5 - (-8)} = -7 \mod 17, \\ & x_R = \lambda^2 - x_P - x_Q = (-7)^2 - (-8) - (-5) = -6 \mod 17, \\ & y_R = \lambda (x_P - x_R) - y_P = -7 \cdot (-8 - (-6)) - 7 = 7 \mod 17, \\ & R = (-6; 7). \\ \end{aligned}$$
- $4A = 2A + 2A = (-5; 3) + (-5; 3) = (-3; 7)$.
- $6A = 3A + 3A = (-6; 7) + (-6; 7) = (-1; 0)$.
- $12A = 6A + 6A = (-1; 0) + (-1; 0) = 0$.
Найденный порядок точки $A = (-8; 7)$ равен 12, следовательно, она является генератором всей группы.
В таблице [tab:elliptic-group-sample] найдены порядки точек и циклические подгруппы группы точек ${{\mathbb{E}}}({{\mathbb{Z}}}_p)$ такой же эллиптической кривой
Группа циклическая, число генераторов:
Циклические подгруппы:
верхний индекс обозначает порядок подгруппы.
| Элемент | Порождаемая группа или подгруппа | Порядок |
| $(-8; \pm 7) $ | Вся группа ${{\mathbb{E}}}({{\mathbb{Z}}}_p)$ | 12, генератор |
| $(-7; \pm 6) $ | Вся группа ${{\mathbb{E}}}({{\mathbb{Z}}}_p)$ | 12, генератор |
| $(-6; \pm 7) $ | ${{\mathbb{G}}}^{(4)} ~=~ \left\{ ~ (-6; \pm 7), ~ (-1; 0), ~ O ~ \right\}$ | 4 |
| $(-5; \pm 3) $ | ${{\mathbb{G}}}^{(6)} ~=~ \left\{ ~ (-5; \pm 3), ~ (-3; \pm 7), ~ (-1; 0), ~ O ~ \right\}$ | 6 |
| $(-3; \pm 7) $ | ${{\mathbb{G}}}^{(3)} ~=~ \left\{ ~ (-3; \pm 7), ~ O ~ \right\}$ | 3 |
| $(-1; 0) $ | ${{\mathbb{G}}}^{(2)} ~=~ \left\{ ~ (-1; 0), ~ O ~ \right\}$ | 2 |
16.7.4. Эллиптические кривые в скрученной форме Эдвардса
Любую эллиптическую кривую с помощью замены координат можно представить в рассмотренной ранее форме Вейерштрасса. Используя данное представление мы ранее ввели операцию сложения точек, умножения точки на число, смогли описать группу точек и циклическую подгруппу. Однако в отдельных случаях эллиптические кривые можно записать в другой, более удобной для частных задач форме. Например, любые эллиптические кривые над алгебраически замкнутым полем можно задать с помощью следующего уравнения:
Примеры кривых, заданных этим уравнениям при различных значениях $d$, приведены на рис. 16.2. Данное кривые в указанном представлении называются эллиптическими кривыми в скрученной форме Эдвардса (англ. Twisted Edwards Curves, [102]).
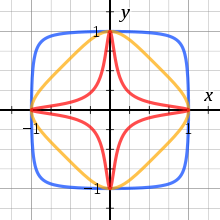
Для данной формы формулы сложения точек задаются одним и тем же способом для любых случаев. В этом важное отличие от формы Вейерштрасса, для которой есть частный случай сложения точки самой с собой (с отдельной формулой вычисления угла наклона касательной). Формулы сложения выглядят так:
При переходе к построению кривых над конечным полем, оказывается, что не все кривые, представимые в форме Вейерштрасса, могут быть представлены в скрученной форме Эдвардса. Для этого необходимо, чтобы порядок кривой $\|E\|$ делился на $4$. Однако если такие кривые использовать для криптографических целей, это даёт значимые преимущества:
- меньшая трудоёмкость операций сложения точек;
- отсутствие частных случаев для формул сложения (усложнение атак по сторонним каналам с различением времени);
16.7.5. Конвертация из скрученной формы Эдвардса в форму Вейерштрасса
Кривая в скрученной форме Эдвардса:
Кривая в форме Вейерштрасса:
Зная коэффициенты $d$ и $e$ кривой в скрученной форме Эдвардса можно найти коэффициенты $a$ и $b$ эквивалентной кривой в форме Вейерштрасса:
И определить правила преобразования координат $(u, v)$ и $(x, y)$ между двумя кривыми:
Нахождение коэффициентов для кривой в скрученной форме Эдвардса по эквивалентной в форме Вейерштрасса является более сложной и нетривиальной задачей, включающей нахождение корней кубического уравнения $x^{3} + ax + b = 0 \mod p$. Кроме того, как было сказано ранее, не все кривые в форме Вейерштрасса имеют эквивалентную кривую в скрученной форме Эдвардса.
16.7.6. Пример группы точек кривой в скрученной форме Эдвардса
Кривая $x^2+y^2=1+6x^2y^2 \mod 11$.
Все точки кривой:
Нейтральным элементом является точка $(0; 1)$.
Данная группа точек является циклической группой, её генератором выступает точка $(2; 5)$ (рис. 16.3):
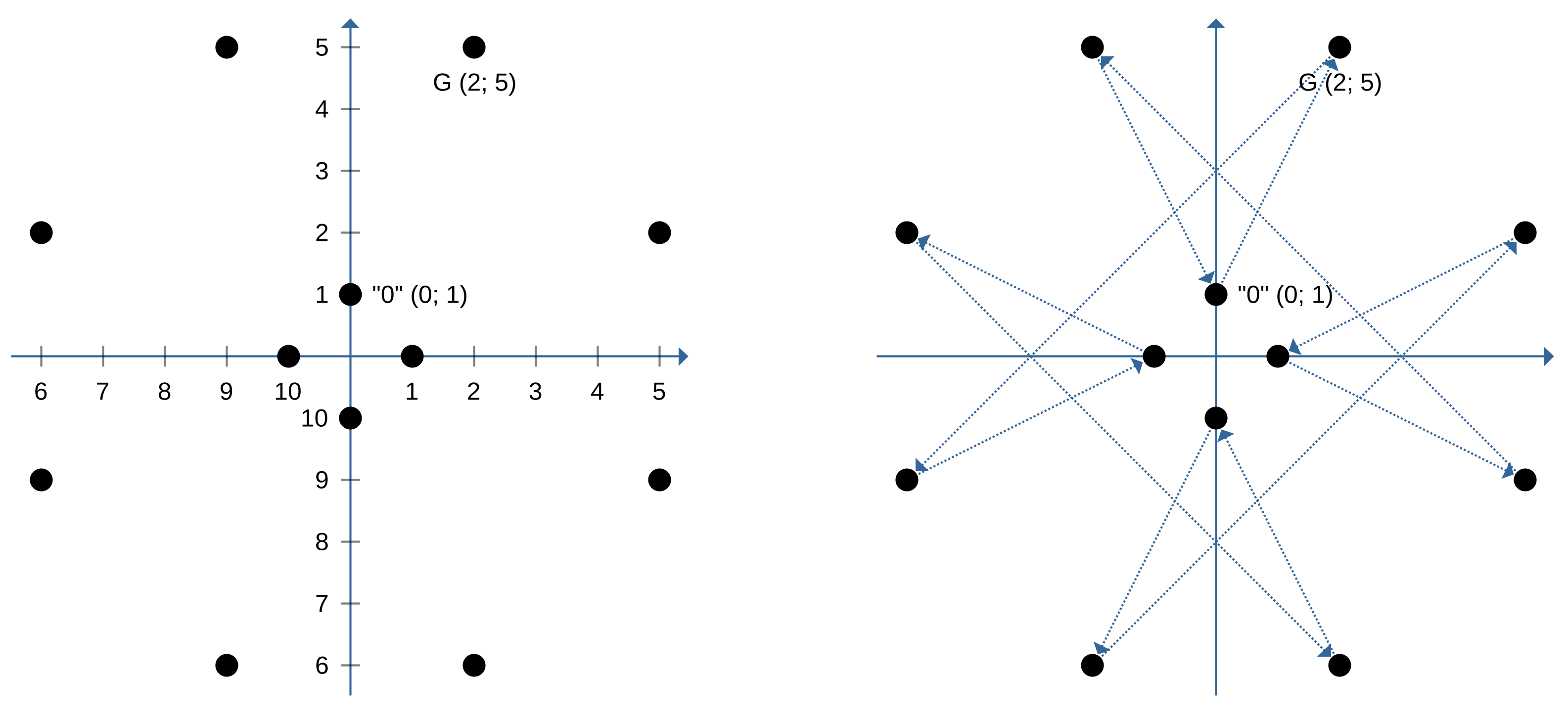
Данная группа изоморфна группе вычетов по сложению ${{\mathbb{Z}}}_{12}$. Можно удостовериться, что сложение двух точек $P (6; 9)$ и $Q(10; 0)$ будет соответствовать результату сложения элементов «2» и «3» в группе ${{\mathbb{Z}}}_{12}$:
Группа не имеет эквивалентной группы точек эллиптической кривой в форме Вейерштрасса над конечным полем ${{\mathbb{F}}}_{11}$. Группа точек соответствующей кривой $y^2 = x^3 + 6 \bmod 11$ имеет только 11 элементов в группе.