5.3. Ячейка Фейстеля
Следующей идеей, продвинувшей развитие блочных шифров и приведшей к появлению государственного стандарта DES, стала конструкция, получившая название ячейка Фейстеля. Данная конструкция приведена на рис. 5.5.
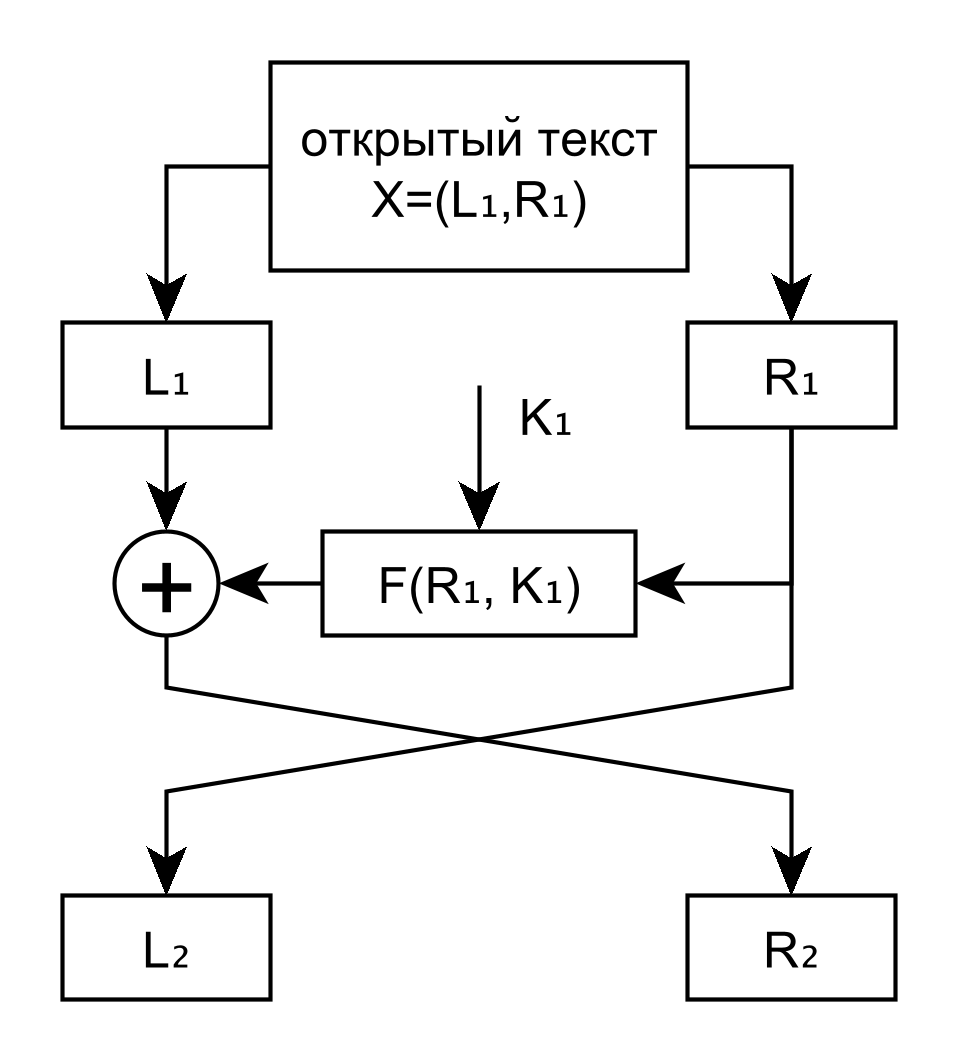
На рис. 5.5 изображён один раунд шифрования блочного шифра, использующего оригинальную ячейку Фейстеля. Каждый раунд шифрования принимает на вход блок с чётным количеством бит и делит его на две равные части $L_k$ и $R_k$. Входным блоком для первого раунда является блок открытого текста. Правая часть $R_k$ без изменений становится левой частью входного блока $L_{k+1}$ следующего раунда шифрования. Кроме того, правая часть подаётся на вход функции Фейстеля $F\left(R_k, K_k \right)$, аргументами которой являются половина блока данных и раундовый ключ (раундовые ключи получаются в результате работы алгоритма ключевого расписания, как описано в разделе 5.1). Результат работы функции Фейстеля складывается с помощью побитового сложения по модулю 2 с левой частью входного блока $L_k$. Полученная последовательность бит становится правой частью выходного блока раунда шифрования. Таким образом, работа $k$-го раунда ячейки Фейстеля описывается следующими соотношениями:
Результатом шифрования является конкатенация последних выходных блоков $L_n$ и $R_n$, где $n$ – число раундов шифрования.
Несложно показать, что зная раундовые ключи $K_1, \dots, K_n$ и результат шифрования $L_n$ и $R_n$, можно восстановить открытый текст. В частности, для каждого раунда:
Таким образом, ячейка Фейстеля гарантирует корректность работы блочного шифра вне зависимости от сложности функции Фейстеля $F\left(R_k, K_k \right)$. В результате криптограф (автор шифра) при использовании ячейки Фейстеля не должен беспокоиться об обратимости функции шифрования в целом (конструкция ячейки Фестеля уже гарантирует это), а должен беспокоиться только о достаточной криптографической стойкости функции Фейстеля, необратимость которой не требуется (и даже вредит криптостойкости). Функция Фейстеля обычно состоит из блоков перестановок и замен (то есть из p- и s-блоков, уже рассмотренных ранее).