6.2. Регистр сдвига с линейной обратной связью

Другой схемой построения псевдослучайных генераторов является использование регистров сдвига с линейной обратной связью, а также её вариациями. Для начала рассмотрим простой РСЛОС, изображённый на рис. 6.1.

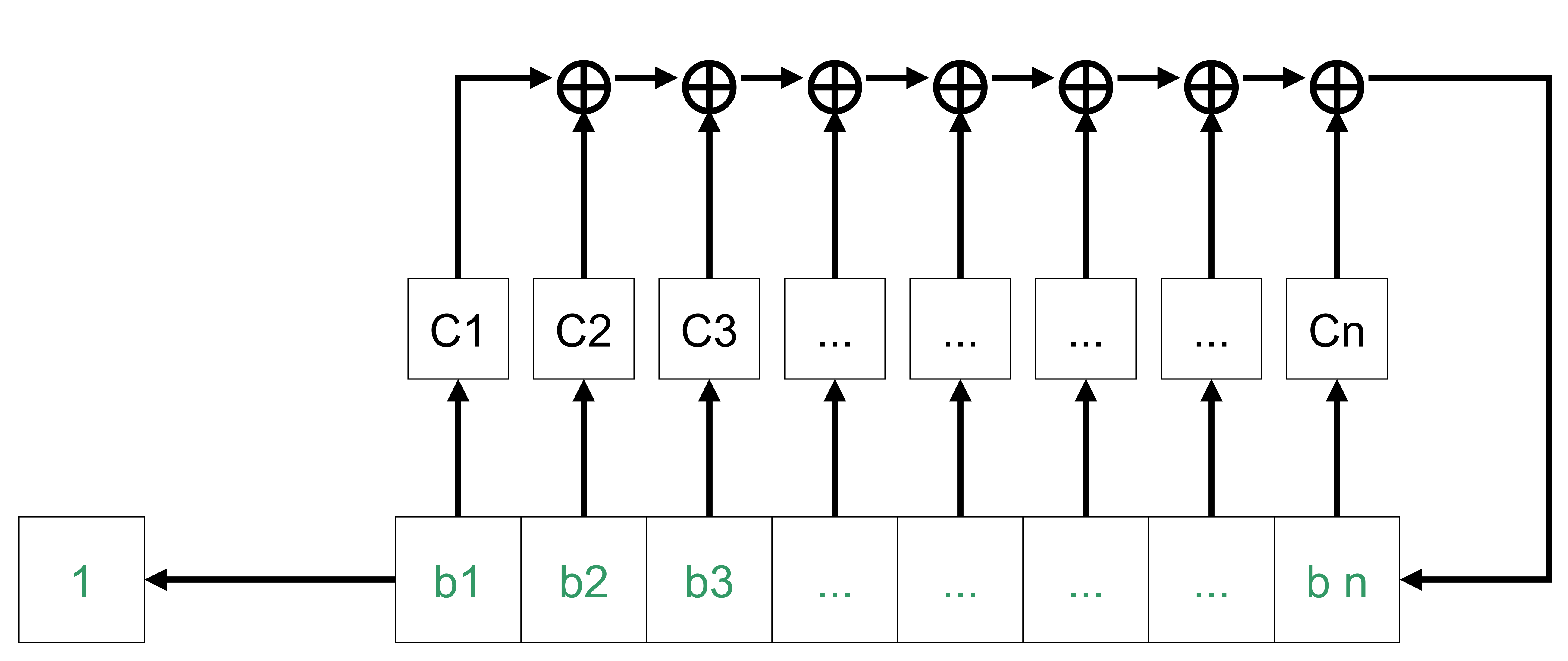
Рис. 6.1 — Регистр сдвига с линейной обратной связью

Регистр сдвига состоит из $n$ однобитовых ячеек $b_1, b_2, \dots, b_n$, содержащих 0 или 1, и линейной обратной связи, определяемой коэффициентами $C_1 = 1$, $C_2, C_3, \dots, C_n \in \{0, 1\}$. Многочлен над полем Галуа $GF(2^n)$ вида $C_1 x^n + C_2 x^{n-1} + \dots + C_n x + 1$ называется характеристическим многочленом РСЛОС.

Начальным состоянием генератора является набор значений в битовых ячейках. На каждой итерации генератор вычисляет сумму по модулю два (то есть выполняет операцию XOR) значений ячеек, для которых $C_i=1$:

$$\begin{array}{ll} b_{n+1} &= \sum\limits_{i} C_i b_i \mod 2, \\ b_{n+1} &= b_1 \oplus C_2 b_2 \oplus C_3 b_3 \oplus \dots \oplus C_n b_n. \end{array}$$

Далее регистр сдвигает значения на одну ячейку влево. Самая правая ячейка $b_n$ принимает вычисленное значение $b_{n+1}$:

$$\begin{array}{ll} b_1 := b_2, \\ b_2 := b_3, \\ \dots \\ b_n := b_{n+1}. \\ \end{array} $$

Выходом генератора является значение ячейки $b_1$ после сдвига.

Пример. Пусть регистр сдвига с линейной обратной связью задан характеристическим многочленом $m\left(x\right)=x^{5} + x^{3} + 1$. Как показано на рисунке, регистр состоит из пяти ячеек. В линейной обратной связи будут участвовать ячейки 1 и 3 (то есть $C_1 = 1, C_3 = 1$, остальные $C_i = 0$).

tikzpicturescale=0.05 black,very thick (30,30) – (30,40) – (40,40) – (40,30) – (30,30) – (30,40); black,thick (35,40) – (35,50) – (35,50) – (37.5,50); black,very thick (40,30) – (40,40) – (50,40) – (50,30) – (40,30) – (40,40); black,very thick (50,30) – (50,40) – (60,40) – (60,30) – (50,30) – (50,40); black,thick (55,40) – (55,47.5); black,thick (53.5,46) – (55,47.5) – (56.5,46); black,thick (37.5,50) – (52.5,50); black,thick (51,51.5) – (52.5,50) – (51,48.5); (55,50) circle radius=2.5; black (52.5,50) – (57.5,50); black (55,47.5) – (55,52.5); black,very thick (60,30) – (60,40) – (70,40) – (70,30) – (60,30) – (60,40); black,very thick (70,30) – (70,40) – (80,40) – (80,30) – (70,30) – (70,40); black,thick (57.5,50) – (85,50) – (85,35) – (80,35); black,thick (82.5,36.5) – (80,35) – (82.5,33.5); black,thick (30,35) – (15,35); black,thick (20,30) – (15,35) – (20,40);

Если начальное состояние регистра равно $\vec{s_0} = (0, 0, 0, 0, 1)$, то дальнейшие внутренние состояния регистра $s_i$ и выходы генератора $r_i$ равны:

$b_{n+1} = b_1 \oplus b_3 = 0 \oplus 0 = 0$, $\vec{s_1} = (0, 0, 0, 1, 0)$, $r_1 = b_1 = 0$;
$b_{n+1} = b_1 \oplus b_3 = 0 \oplus 0 = 0$, $\vec{s_2} = (0, 0, 1, 0, 0)$, $r_2 = b_1 = 0$;
$b_{n+1} = b_1 \oplus b_3 = 0 \oplus 1 = 1$, $\vec{s_3} = (0, 1, 0, 0, 1)$, $r_3 = b_1 = 0$;
$b_{n+1} = b_1 \oplus b_3 = 0 \oplus 0 = 0$, $\vec{s_4} = (1, 0, 0, 1, 0)$, $r_4 = b_1 = 1$;
$b_{n+1} = b_1 \oplus b_3 = 1 \oplus 0 = 1$, $\vec{s_5} = (0, 0, 1, 0, 1)$, $r_5 = b_1 = 0$;
$b_{n+1} = b_1 \oplus b_3 = 0 \oplus 1 = 1$, $\vec{s_6} = (0, 1, 0, 1, 1)$, $r_6 = b_1 = 0$;
$b_{n+1} = b_1 \oplus b_3 = 0 \oplus 0 = 0$, $\vec{s_7} = (1, 0, 1, 1, 0)$, $r_7 = b_1 = 1$;
$b_{n+1} = b_1 \oplus b_3 = 1 \oplus 1 = 0$, $\vec{s_8} = (0, 1, 1, 0, 0)$, $r_8 = b_1 = 0$; и так далее.

Максимальный период последовательности РСЛОС равен $2^n - 1$. Максимум достигается в том и только в том случае, когда характеристический многочлен РСЛОС примитивен. В этом случае РСЛОС называют регистром сдвига максимального периода, а генерируемые им последовательности – М-последовательностями или же последовательностями максимального периода.

Если известна структура РСЛОС (значения коэффициентов $C_2, \dots, C_n$), то внутреннее состояние генератора можно восстановить по $n$ предыдущим выходам. По $2n$ предыдущим выходам генератора можно восстановить и внутреннее состояние, и структуру генератора. Зная структуру и текущее внутреннее состояние генератора, можно восстановить его предыдущие и следующие выходные значения.