6.4. КСГПСЧ на основе РСЛОС
Как уже упоминалось ранее, использование РСЛОС в качестве ГПСЧ не является криптографически стойким. Однако можно использовать комбинацию из нескольких регистров сдвига, чтобы в результате получить быстрый, простой (дешёвый) и надёжный (криптографически стойкий) генератор псевдослучайных чисел.
6.4.1. Генераторы с несколькими регистрами
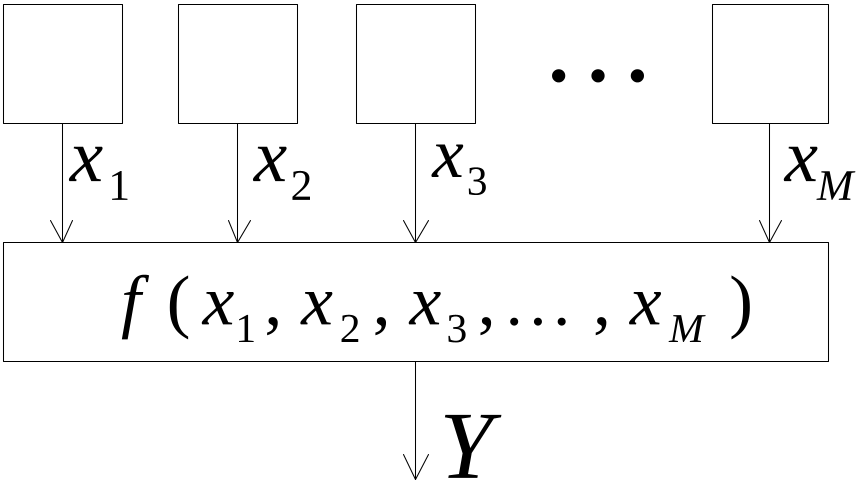
Первый способ улучшения криптографических свойств последовательности состоит в создании композиционных генераторов из нескольких регистров сдвига при определённом способе выбора параметров. Схема такого генератора показана на рис. 6.2. Здесь $L_i, ~ i = 1, 2, \dots, M$ – регистры сдвига с линейной обратной связью. Вырабатываемые ими двоичные символы $x_{1,i}, x_{2,i}, \dots, x_{M,i}$ поступают синхронно на устройство преобразования, задаваемое булевой функцией $f(x_{1,i}, x_{2,i}, \dots, x_{M,i})$. В булевой функции и аргументы, и значения функции принимают значения $0$ или $1$.
Число ячеек в $i$-м регистре равно $L_{i}$, причём $\gcd(L_i, L_j)=1$ для $i \neq j$, где $\gcd$ – наибольший общий делитель. Общее число ячеек $L = \sum\limits_{i=1}^M L_i$. Булева функция $f$ должна включать слагаемое по одному из входов, то есть $f = \dots + x_i + \dots$, для того чтобы двоичные символы на выходе этой функции были равновероятными. Период этого генератора может достигать величины (немного меньше)

Таким образом, увеличение числа регистров сдвига с обратной связью увеличивает период последовательности.
Одним из способов оценки криптостойкости генератора является оценка длины регистра с линейной обратной связью, эквивалентного по порождаемой последовательности. Такой эквивалентный РСЛОС находится с помощью алгоритма Берлекэмпа — Мэсси декодирования циклических кодов. В лучшем случае длина эквивалентного регистра соизмерима с периодом последовательности, порождённой нелинейным генератором. В общем случае определение эквивалентной длины является сложной задачей.
6.4.2. Генераторы с нелинейными
Известно, что любая булева функция $f(x_1, x_2, \dots, x_M)$ может быть единственным образом записана многочленом Жегалкина:
Второй способ улучшения криптостойкости последовательности поясняется с помощью рис. 6.3, на котором представлены регистр сдвига с $M$ ячейками и устройство, осуществляющее преобразование с помощью булевой функции $f(x_1, x_2, \dots, x_M)$, причём функция $f$ содержит нелинейные члены, то есть произведения $x_i x_j \dots$. Тактовый вход здесь такой же, как у регистров, показанных на других рисунках.
Если функция $f$ нелинейная, то в общем случае неизвестен полиномиальный алгоритм восстановления состояния регистров по нескольким последним выходам генератора. Таким образом, использование нескольких регистров сдвига увеличивает максимально возможный период, по сравнению с одним регистром, до $T < 2^{L_1 + L_2 + \dots + L_M}$, а нелинейность функции $f$ позволяет избежать простого нахождения состояния по выходу. Чтобы улучшить криптостойкость последовательности, порождаемой регистром, рекомендуется брать много нелинейных членов многочлена Жегалкина.
Такой подход применён в системе GPS. Удачных попыток её взлома до сих пор нет.
6.4.3. Мажоритарные генераторы на примере алгоритма шифрования A5/1
Третий способ улучшения криптостойкости последовательностей поясняется с помощью рис. 6.4, на котором показан мажоритарный генератор ключей алгоритма потокового шифрования A5/1 стандарта GSM. В отличие от случая нелинейного комбинирования выходов нескольких регистров в этом случае применён условный сдвиг регистров, то есть на каждом такте некоторые регистры могут не сдвигаться, а оставаться в прежнем состоянии. На рисунке показана схема из трёх регистров сдвига с различными многочленами обратной связи (здесь применена обратная нумерация ячеек, коэффициентов и переменных по сравнению с предыдущими разделами):
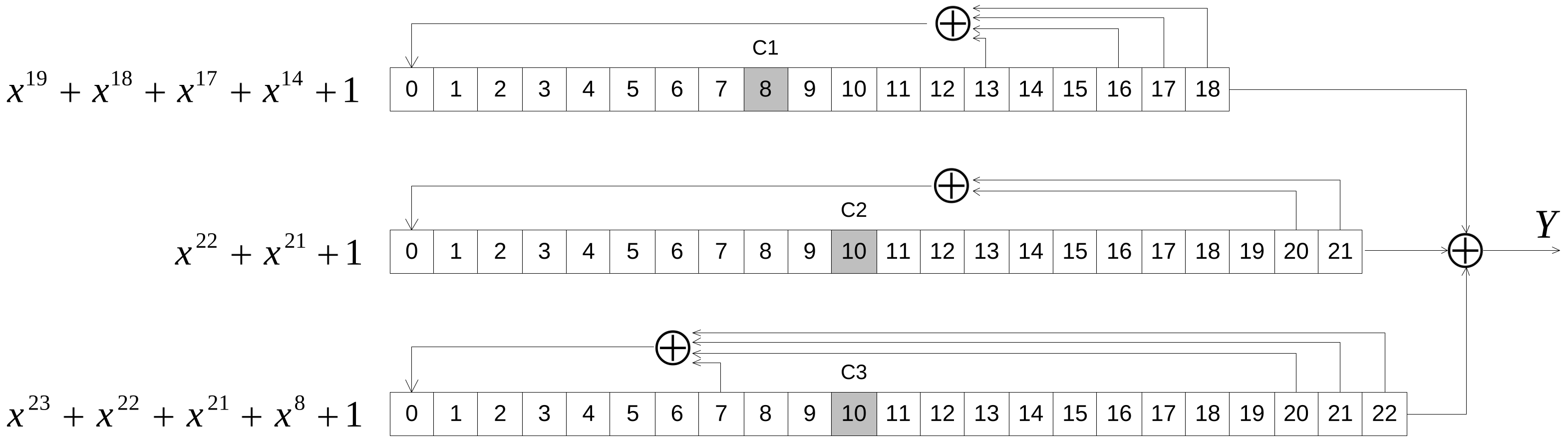
В алгоритме A5/1 регистры сдвигаются не на каждом такте. Правило сдвига следующее. В каждом регистре есть один тактовый бит, определяющий сдвиг, – восьмой бит $\textrm{C1}$ для первого регистра, десятые биты $\textrm{C2}$ и $\textrm{C3}$ для второго и третьего регистров. На каждом такте вычисляется мажоритарное значение тактового бита $m = \textrm{majority}(\textrm{C1}, \textrm{C2}, \textrm{C3})$, то есть по большинству значений: 0 или 1. Если для данного регистра значение тактового бита совпадает с мажоритарным решением, то регистр сдвигается. Если не совпадает, то остаётся в прежнем состоянии без сдвига на следующий такт. Так как всего состояний тактовых битов $2^3$, то в среднем каждый регистр сдвигается в $\frac{3}{4}$ всех тактов.
Общее количество ячеек всех трёх регистров $19+22+23=64$, следовательно, период генератора A5/1: $T < 2^{64}$. Данный шифр не может считаться стойким из-за возможности полного перебора. Например, известны атаки на шифр A5/1, требующие 150-300 GiB оперативной памяти и нескольких минут вычислений одного ПК (2001 г.).