8.1. Структура Меркла — Дамгора

Приведём пример метода построения хеш-функции, называемого структурой (конструкцией, методом) Меркла — Дамгора (рис. 8.1), впервые описанной в кандидатской диссертации Ральфа Меркла в 1979 году. Меркл и Дамгор независимо друг от друга показали, что если раундовая функция сжатия (обозначенная $f$ на рис. 8.1) устойчива к коллизиям, то итоговая хеш-функция будет также устойчива (англ. Ralph Charles Merkle, дат. Ivan Bjerre Damgård, [26, 71, 72]).

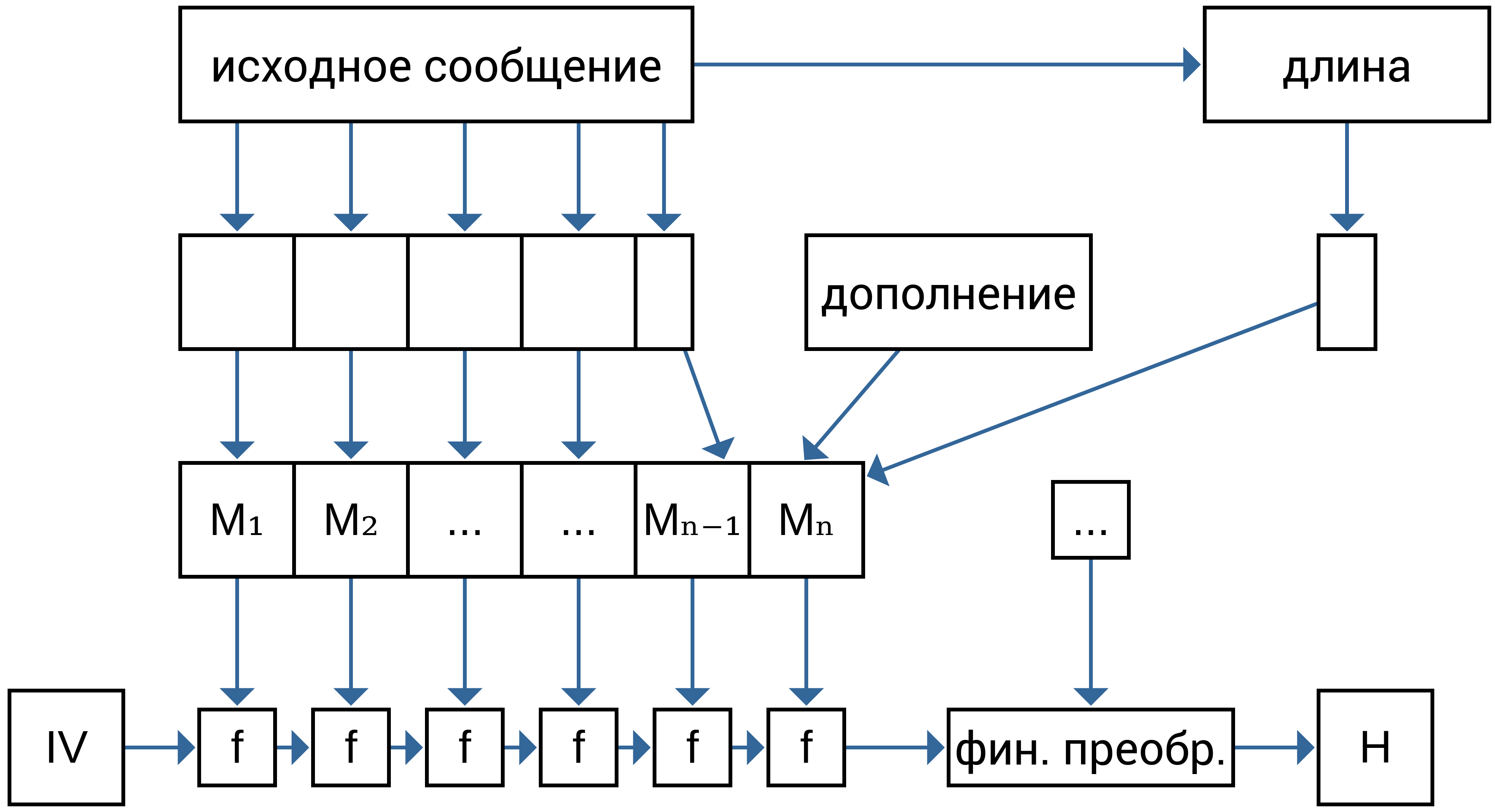
Пусть есть задан открытый текст $M$ в виде двоичной последовательности некоторой длины. Текст дополняется, во-первых, дополнением (паддингом), во-вторых, длиной исходного сообщения таким образом, чтобы после дополнения обрабатываемая последовательность можно было разбить на целое число блоков фиксированной длины $M_1, M_2, \dots, M_n$.

Выбирается некоторый начальный вектор IV. Далее последовательно применяется раундовая функция сжатия к двум аргументам, первым из которых является рещультат предыдущего вызова (IV для самого первого), а вторым аргументом – соответствующий блок $M_i$ обрабатываемой последовательности.

$$\begin{array}{l} H_0 = \text{IV},\\ H_i = f ( H_{i-1}, M_i ).\\ \end{array}$$

В зависимости от хеш-функции структура может быть дополнена финальным преобразованием, в котором вторым аргументом будет ещё одна некоторая функция от исходного сообщения. Например, в хеш-функции «Стрибог» таким аргументом является арифметическая функция всех блоков исходного открытого текста.

К плюсам данной конструкции относят доказанный авторами факт, что если раундовая функция сжатия устойчива к коллизиям, то итоговая хеш-функция будет также устойчива. Однако у конструкции присутствуют и недостатки.

Атака на нахождение второго прообраза (для некоторого известного открытого текста) может быть выполнена за $2^n / | M |$ операций, где $| M |$ – длина открытого текста. Это меньше, чем требуется операций для полного перебора ($2^n$), особенно для длинных сообщений.
Если известен способ нахождения пары коллизий, то множественные коллизии найти незначительно сложнее.
В отсуствие финального преобразования при заданном значении хеш-функции $h = H(M)$ (и неизвестном исходном сообщении $M$) можно легко найти значение $H( pad(M) \| M' )$, где $pad(M)$ – функция дополнения, а $M'$ – выбранный злоумышленником дополнительный текст к исходному сообщению.

С использованием данной конструкции построены такие криптографические хеш-функции, как MD4, SHA-1, SHA-2, российский стандарт ГОСТ Р 34.11-2012 («Стрибог») и многие другие.