8.5. Имитовставка (MAC)

Для обеспечения целостности и подтверждения авторства информации, передаваемой по каналу связи, используют имитовставку ${\textrm{MAC}}$ (англ. Message Authentication Code).

displayquote Имитовставка, код аутентичности сообщения (англ. message authentication code, seal, integrity check value) — в протоколах аутентификации сообщений с доверяющими друг другу участниками — специальный набор символов, добавляемый к сообщению и предназначенный для обеспечения его целостности и аутентификации источника данных. flushrightСловарь криптографических терминов [132]

Далее под имитовставкой мы будем понимать некоторую ключевую функцию (класс функций) ${\textrm{MAC}}(K,m)$

$$ \textrm{MAC}: \{0,1\}^{|K|} \times \{0,1\}^* \to \{0,1\}^{|MAC|}, $$

зависящую от передаваемого сообщения $m$ и некоторого ключа $K$ отправителя $A$, обеспечивающую свойства аутентификации сообщения:

свойство корректности получатель $B$, используя такой же или другой связанный ключ, имеет возможность проверить целостность и доказать принадлежность информации участнику, знающему ключ $K$В случае использования симметричной криптографии участник $B$ знает секретный ключ $K$ и доказать авторство отправителя $A$ он может только самому себе. При попытке доказать другому участнику оригинальный отправитель $A$ может отрицать авторство сообщения и настаивать, что имитовставку сгенерировал получатель $B$, так как он тоже знает секретный ключ $K$.;
свойство надёжности злоумышленник (криптоаналитик) не может (за обозримое время или же в принципе) сфальсифицировать значение имитовставки, то есть сгенерировать новое сообщение или модифицировать старое таким образом, чтобы получатель $B$ некорректно принял сообщение как от отправителя $A$ с вероятностью, больше заданной.

Имитовставка может быть построена либо на симметричной криптосистеме (в таком случае обе стороны имеют один общий секретный ключ), либо на криптосистеме с открытым ключом, в которой $A$ использует свой секретный ключ, а $B$ – открытый ключ отправителя $A$.

8.5.1. HMAC

Наиболее универсальный способ аутентификации сообщений с использованием схем ЭЦП на криптосистемах с открытым ключом состоит в том, что сторона $A$ отправляет стороне $B$ сообщение

$$ m ~\|~ \textrm{ЭЦП}(K, h(m)), $$

где $h(m)$ – криптографическая хеш-функция в схеме ЭП и $\|$ является операцией конкатенации битовых строк. Для аутентификации большого объёма информации этот способ не подходит из-за медленной операции вычисления подписи. Например, вычисление одной ЭЦП на криптосистемах с открытым ключом занимает порядка 10 мс на ПК. При средней длине IP-пакета 1 Кбайт, для каждого из которых требуется вычислить имитовставку, получим максимальную пропускную способность в $\frac{1 ~ \text{Кбайт}}{10 ~ \text{мс}} = 100$ Кбайт/с.

Поэтому для большого объёма данных, которые нужно аутентифицировать, $A$ и $B$ создают общий секретный ключ аутентификации $K$. Далее имитовставка вычисляется либо с помощью модификации блочного шифра, либо с помощью криптографической хеш-функции.

Для каждого пакета информации $m$ отправитель $A$ вычисляет ${\textrm{MAC}}(K,m)$ и присоединяет его к сообщению $m$:

$$ m ~ \|~ {\textrm{MAC}}(K,m). $$

Зная секретный ключ $K$, получатель $B$ может удостовериться с помощью кода аутентификации, что информация не была изменена или фальсифицирована, а была создана отправителем.

Требования к длине кода аутентификации в общем случае такие же, как и для криптографической хеш-функции, то есть длина должна быть не менее 160--256 бит. На практике часто используют усечённые имитовставки.

Стандартные способы использования имитовставки сообщения следующие.

Если шифрование данных не применяется, отправитель $A$ для каждого пакета информации $m$ отсылает сообщение
$$ m ~\|~ {\textrm{MAC}}(K, m) .$$
Если используется шифрование данных симметричной криптосистемой с помощью ключа $K_e$, то имитовставка с ключом $K_a$ может вычисляться как до, так и после шифрования:
$$ E_{K_e}(m) ~\|~ {\textrm{MAC}}(K_a, E_{K_e}(m)) ~~ \text{ или } ~~ E_{K_e}(m ~\|~ {\textrm{MAC}}(K_a, m)). $$

Первый способ, используемый в IPsec, хорош тем, что для проверки целостности достаточно вычислить только имитовставку, тогда как во втором случае перед проверкой необходимо дополнительно расшифровать данные. С другой стороны, во втором способе, используемом в системе PGP, защищённость имитовставки не зависит от потенциальной уязвимости алгоритма шифрования.

Вычисление имитовставки от пакета информации $m$ с использованием блочного шифра $E$ осуществляется в виде:

$$ {\textrm{MAC}}(K, m) = E_K(H(m)), $$

где $H$ – криптографическая хеш-функция.

Имитовставка на основе хеш-функции обозначается ${\textrm{HMAC}}$ (англ. Hash-based MAC) и стандартно вычисляется в виде:

$$ {\textrm{HMAC}}(K, m) = H(K \| H(K \| m)). $$

Возможно также вычисление в виде:

$$ {\textrm{HMAC}}(K, m) = H(K \| m \| K). $$

В протоколе IPsec используется следующий способ вычисления кода аутентификации:

$$ {\textrm{HMAC}}(K, m) = H((K \oplus ~ \textrm{opad}) ~\|~ H((K \oplus ~ \textrm{ipad}) ~\|~ m)), $$

где $\textrm{opad}$ – последовательность повторяющихся байтов

$$ \text{\texttt{0x5C}}= [01011100]_2, $$

$\textrm{ipad}$ – последовательность повторяющихся байтов

$$ \text{\texttt{0x36}} = [00110110]_2, $$

которые инвертируют половину битов ключа. Считается, что использование различных значений ключа повышает криптостойкость.

В протоколе защищённой связи SSL/TLS, используемом в интернете для инкапсуляции, в том числе, протокола HTTP в протокол HTTPS, код ${\textrm{HMAC}}$ определяется почти так же, как в IPsec. Отличие состоит в том, что вместо операции XOR для последовательностей $\textrm{ipad}$ и $\textrm{opad}$ осуществляется конкатенация:

$$ {\textrm{HMAC}}(K, m) = H((K ~\|~ \textrm{opad}) ~\|~ H((K ~\|~ \textrm{ipad}) ~\|~ m)). $$

Двойное хеширование с ключом в

$$ {\textrm{HMAC}}(K, m) = H(K \| H(K \| m)) $$

применяется для защиты от атаки на расширение сообщений. Вычисление хеш-функции от сообщения $m$, состоящего из $n$ блоков $m_{1}, m_2 \dots m_n$, можно записать в виде:

$$\begin{array}{l} m \equiv m_1 \Vert m_2 \Vert \dots \Vert m_n, \\ H_0 \equiv IV = \textrm{const}, \\ H_i = f(H_{i-1}, m_i), i \in \{ 1, 2, \dots, n \},\\ H(m) \equiv H_n, \end{array}$$

где $f$ – известная сжимающая функция.

Пусть имитовставка использует одинарное хеширование с ключом:

$$ {\textrm{MAC}}(K, m) = H(K \| m) = H (m_0 = K \| m_1 \| m_2 \| \dots \| m_n). $$

Тогда криптоаналитик, не зная секретного ключа, имеет возможность вычислить имитовставку для некоторого расширенного сообщения $m \| m_{n+1}$:

$$ {\textrm{MAC}}(K, m \| m_{n+1}) = \underbrace{H \left( K \| m_1 \| m_2 \| \dots \| m_n \right.}_{{\textrm{MAC}}(K, m)} \left. \| m_{n+1} \right) = $$

$$ = f({\textrm{MAC}}(K, m), m_{n+1}). $$

8.5.2. Универсальное хеширование

Наличие одного единственного правила хеширования может привести к тому, что злоумышленник, зная точную формулу вычисления хеша, сможет подобрать такой набор входных данных, который с большой степенью вероятности даёт коллизии обычной (не криптографической) хеш-функции. Кроме того, сами хеш-функции также разрабатываются исходя из определённого предположения о входных данных. Алгоритмы хеширования могут содержать некоторые константы, которые разработчику информационной системы предлагается выбрать самостоятельно, основываясь на его предположениях об особенностях входных данных. Но квалификации разработчика, либо его априорных знаний, может не хватать для эффективного выбора конкретной реализации (алгоритм и параметры) хеширования. Исходя из этого Картер и Вегман в 1979 году (англ. John Lawrence Carter, Mark N. Wegman, [23]) предложили определить класс алгоритмов хеширования с возможностью выбора одного из них непосредственно в момент вызова.

Обозначим через $\delta$ возможный факт совпадения значения некоторой унарной функции для некоторых значений аргументов:

$$ \delta_{f}( x, y ) = \left\{\begin{matrix} 1, & f(x) = f(y);\\ 0, & f(x) \neq f(y). \end{matrix}\right. $$

Пусть $H$ – класс функций, преобразующих $M \to R$. Будем называть класс $H$ универсальным$_{2}$, если

$$ \forall x, y \in M: \sum_{h \in H} \delta_{h}( x, y ) \leq |H| / |R|. $$

То есть класс функций $H$ универсален$_{2}$, если для любых пар аргументов $x$ и $y$ значения функций совпадают не более чем для $1/|R|$-ой части функций из множества $H$. Нижний индекс «$_{2}$» подчёркивает тот факт, что речь идёт о совпадении значений только для пар элементов. В дальнейшем мы его будем опускать.

Примеры универсальных классов для хеширования:

Универсальность первых двух примеров была показана ещё в работе Картера и Вегмана [23]. Последний описан, например, в [84].

функции хеширования для чисел $x$
$$ \begin{array}{l} h(x) = ax + b \bmod p,\\ a \in {{\mathbb{Z}}}^*_p, b \in {{\mathbb{Z}}}_p;\\ \end{array} $$
функции хеширования для векторов $\vec{x}$
$$ \begin{array}{l} \vec{x} = \left \langle x_0, x_1, \dots, x_r \right \rangle,\\ \vec{a} = \left \langle a_0, a_1, \dots, a_r \right \rangle,\\ \forall i \in {{\mathbb{Z}}}_{r+1}: a_i \in {{\mathbb{Z}}}_{p},\\ h( \vec{x} ) = \sum_{i=0}^{r} a_i x_i \bmod p;\\ \end{array} $$
функции хеширования для строк (последовательностей переменной длины) $\vec{x}$
$$ \begin{array}{l} \vec{x} = \left \langle x_0, x_1, \dots, x_l \right \rangle,\\ \forall x_i: x_i \in {{\mathbb{Z}}}_{u}, \\ p \geq u, \\ a \in {{\mathbb{Z}}}_{p}, a \neq 0,\\ h( \vec{x} ) = \sum_{i=0}^{l} a^{i} x_i \bmod p.\\ \end{array} $$

На основе универсального хеширования построены такие криптографические примитивы, как UMAC и Poly1305 (RFC 8439).

8.5.3. Одноразовая имитовставка

Одноразовый MAC (англ. One-Time MAC) можно рассматривать как аналог одноразового шифрблокнота для целей аутентификации сообщения. Если использовать один ключ для ровно одного сообщения, можно построить код аутентификации, который гарантированно не может быть подделан злоумышленником.

Если сообщение короткое, то можно считать ключом два числа $a$ и $b$, а в качестве значения MAC для сообщения $m \in M$ будет выступать

$$ h(m) = a \times m + b \bmod p. $$

Если $p$ – простое, то вероятность угадать значение MAC для некоторого сообщения $m_2$ (то есть подменить сообщение $m_1$ с одновременной генерацией нового MAC) без знания ключа $k=\overrightarrow{(a,b)}$, равна строго $1/p$.

Можно воспользоваться описанной ранее функцией хеширования для сообщений переменной длины и использовать чуть более сложную формулу для вычисления MAC:

$$ \begin{array}{l} \vec{m} = \left \langle m_1, m_2, \dots, m_l \right \rangle, \\ h(\vec{m}) = b + \sum_{i=1}^{l} a^i m_i \mod p. \\ \end{array} $$

Для этой формулы по прежнему сохраняется свойство, что если ключ $k=\overrightarrow{(a,b)}$ используется ровно один раз, злоумышленник не сможет подделать (угадать) MAC с вероятностью более $1/p$.

8.5.4. Конструкция Вегмана-Картера

В 1981 году Вегман и Картер предложили ([108]) использовать универсальное хеширование (раздел 8.5.2) для построение алгоритмов имитовставок. В оригинале авторы предполагали, что каждое сообщение содержит неповторяющийся номер $i$, а секретный ключ между отправителем и получателем состоит из двух частей:

параметра $k_1$, задающего способ выбора функции из универсального класса хеширования $H: K \times A \to B$;
параметра $k_2$, который является последовательностью строк $b_1, b_2, \dots, b_n$, длина каждой из которых совпадает с размером элементов множества $B$.

Результатом вычисления имитовставки является:

$$ \begin{array}{l} m' = \langle i, m \rangle,\\ \textrm{MAC} (m') = H_{k_1}(m) \oplus b_i. \end{array} $$

Авторы показали надёжность данной схемы при условии случайного выбора ключей и универсальности класса хеширования. Однако с практической точки зрения использовать ключи, состоящие из последовательностей очень непрактично. Более того, можно было передать столько сообщений, сколько элементов последовательности задано в $k_2$. Для передачи сообщения сверх этого лимита нужно было либо расширить существующий ключ, либо сгенерировать новый.

По этой причине сейчас вместо использования последовательности строк $b_1, b_2, \dots, b_n$ в качестве ключа предполагается наличие некоторого класса псевдослучайных функций (англ. pseudorandom function family, PRF), который эмулирует случайного оракула. В своей идеализированной модели он для каждого некоторого входа может выдать ответ, случайно распределённой по области значений. Однако если на вход случайного оракула будет подано уже ранее подававшееся значение, он должен выдать прежний ответ. Входом этого оракула являются, во-первых, некоторое случайное число $r$, которое заменило собой номер сообщения, во-вторых часть общего секретного ключа $k_2$, которая будет служить для выбора конкретной функции из класса псевдослучайных.

В качестве практической реализации такого класса функций могут, с некоторым приближением, выступать другие реализации имитовставок, даже если они медленно работают. Например, основанные на криптографических хеш-функциях или блочных шифрах. Потому что им на вход (в отличие от быстрой функции универсального хеширования) подаётся только небольшой блок информации – случайное число $r$.

Таким образом, современную конструкцию Вегмана-Картера можно описать так. Пусть выбран некоторый класс универсальных хеш-функций (например, в качестве него можно использовать одноразовую имитовставку из раздела 8.5.3)

$$ H: \{0,1\}^{|k_1|} \times \{0,1\}^* \to \{0,1\}^n, $$

и некоторая надёжная реализация медленной имитовставки

$$ PRF: \{0,1\}^{|k_2|} \times \{0,1\}^{|r|} \to \{0,1\}^n. $$

Тогда получение быстрой имитовставки можно сделать следующим образом

$$ \begin{array}{l} \textrm{secret key: } k: \langle k_1, k_2 \rangle,\\ \textrm{random nonce: } r \leftarrow \{0,1\}^n,\\ \textrm{MAC} (m) = \langle r, H_{k_1}(m) \oplus PRF_{k_2}(r) \rangle. \end{array} $$

Как утверждается в [57], использование данной конструкции позволяет достичь скорости хеширования в $0{,}5$ циклов процессора на один байт сообщения (англ. cycles per byte, cpb).

8.5.5. UMAC

Конструкция UMAC, предложенная в 1999 году ([103]), также использует подход с быстрым универсальным хешированием большого исходного сообщения и хешированием небольшого блока информации надёжной (на 1999 год), но медленной ключевой функцией HMAC-SHA1. В 2003 году вошёл в список алгоритмов, отобранных инициативой NESSIE (англ. New European Schemes for Signatures, Integrity, and Encryptions) как безопасный алгоритм вычисления имитовставки. В 2006 году был стандартизован как RFC 4418 ([104]). На сегодняшний день не считается криптографически стойким из-за уязвимостей, найденных в SHA-1.

Используемый в UMAC универсальный$_2$ класс хеш-функций $\textrm{NH}_K (m)$ описывается следующим образом. Битовая строка $m$ длиной до 1024 32-битовых «слов» и размером, кратная 2 «словам», разбивается на отдельные блоки по 32 бита $m_1, m_2, \dots, m_l$. 32-битные ключи $K_1, K_2, \dots, K_l$ получаются из исходного ключа $K$ с помощью генератора псевдослучайных чисел. Далее вычисление 64-битового хеша выглядит так:

$$\begin{array}{ll} \textrm{NH}_K (m) = & ( m_1 +_{32}K_1) \times_{64} (m_2 +_{32} K_2) +_{64} \dots \\ & \dots ~ +_{64} ~ \dots \\ & \dots ~ +_{64} ~ (m_{l-1} +_{32} K_{l-1}) \times_{64} (m_l+_{32}K_l), \end{array} $$

где $+_{32}$ – сложение 32-битных строк, в результате которого получается 32-битная сумма, $\times_{64}$ – произведение двух 32-битных строк, и получаемый 64-битный результат умножения (рис. 8.11).

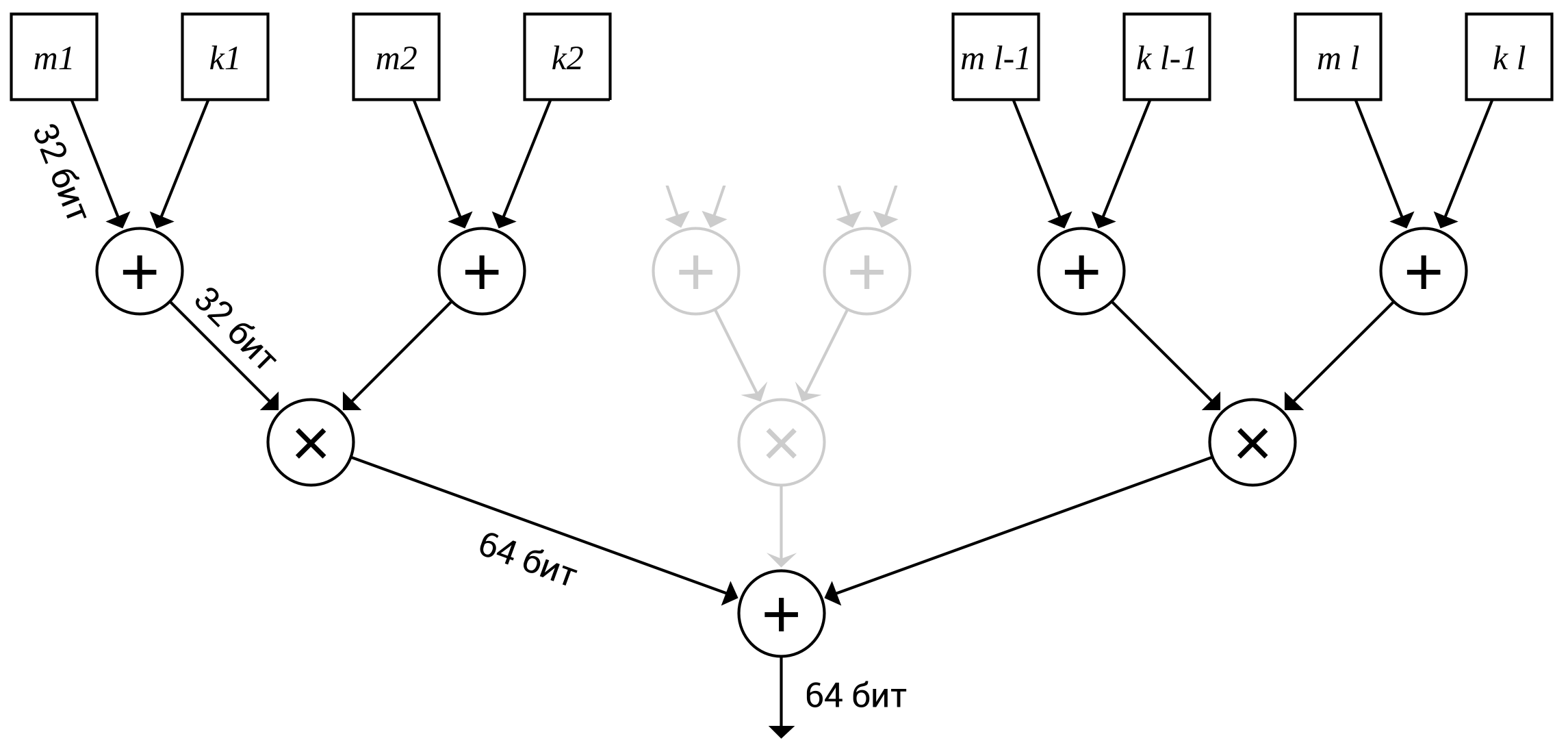
Рис. 8.11 — Универсальное хеширование $\textrm{NH}_K (m)$ в UMAC

Генерация имитовставки делается следующим образом. Предполагается, что вместе с сообщением $m$ передаётся случайная строка nonce (должна быть уникальна для каждого сообщения), а у отправителя и получателя есть общий секретный ключ $K$.

Пусть Len это остаток от деления длины сообщения в битах $|m|$ на 4096:
$$ \textrm{Len} = |m| \bmod 4096. $$
Сообщение $m$ в битовом представлении дополняется нулями таким образом, чтобы длина сообщения $|m|$ была кратна 64 бит (8 байт).
Сообщение $m$ разбивается на блоки по 32768 бита (1024 «слова» по 32 бита) $m_1, m_2, \dots, m_t$. Последний блок будет содержать от 2 до 1024 «слов».
Каждый блок хешируется ключевой хеш-функцией $\textrm{NH}_K$, результаты конкатенируются между собой и $Len$:
$$ H_K(m) = \textrm{NH}_K (m_1) ~ \| ~ \textrm{NH}_K (m_2) ~ \| ~ \dots ~ \| ~ \textrm{NH}_K (m_t) ~ \| ~ \textrm{Len}. $$
Итоговое значение имитовставки получается через хеширование ключевой функцией HMAC-SHA1:
$$ \textrm{UMAC}_K( m, \textrm{nonce} ) = \textrm{HMAC-SHA1}_K( \textrm{nonce} ~ \| ~ H_K(m) ). $$