Глава 12. Разделение секрета
12.1. Пороговые схемы
Идея пороговой $(K, N)$-схемы разделения общего секрета среди $N$ пользователей состоит в следующем. Доверенная сторона хочет распределить некий секрет $K_0$ между $N$ пользователями таким образом, что:
- любые $m_1: K \leq m_1 \leq N$, легальных пользователей могут получить секрет (или доступ к секрету), если предъявят свои секретные ключи;
- любые $m_2: m_2 < K$, легальных пользователей не могут получить секрет и не могут определить (вычислить) этот секрет, даже решив трудную в вычислительном смысле задачу.
Далее рассмотрены три случая: $(K, N)$-схема Блэкли, $(K, N)$-схема Шамира и простая $(N,N)$-схема.
12.1.1. Схема разделения секрета Блэкли
Схема разделения секрета Блэкли (англ. George Robert Blakley, [15], рис. 12.1), также называемая векторной схемой, основывается на том, что для восстановления всех координат точки в $K$-мерном пространстве, принадлежащей нескольким неколлинеарным гиперплоскостям, необходимо и достаточно знать уравнения $K$ таких плоскостей. То есть в двумерном пространстве нужны две пересекающиеся прямые, в трёхмерном – три пересекающиеся в нужной точке плоскости и так далее.
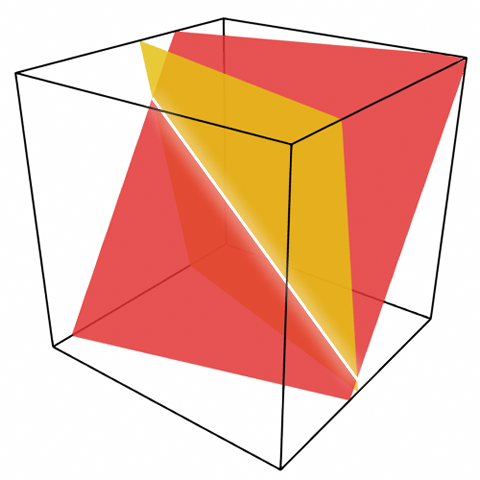
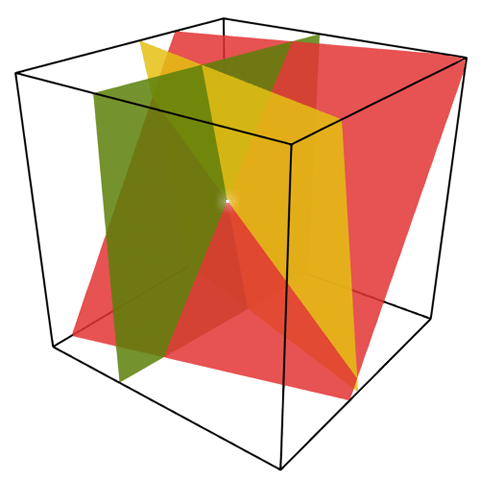
Для разделения секрета $M$ между $N$ сторонами таким образом, чтобы любые $K$ сторон могли восстановить секрет, доверенный центр выполняет следующие операции:
- выбирает несекретное большое простое число $p$ ($p > M$);
- выбирает случайную точку, одна из координат которой (например, первая) будет равна разделяемому секрету $M$: $(x_1 = M, x_2, \dots, x_K)$;
- для каждого участника $i$ выбирает $K$ случайных коэффициентов гиперплоскости $C^i_1, C^i_2, \dots, C^i_{K}$ ($\ne 0$), а последний коэффициент $C^i_{K+1}$ вычисляется таким образом, чтобы гиперплоскость проходила через выбранную точку:
$$ \begin{array}{l} C^i_1 x_1 + C^i_2 x_2 + \dots + C^i_K x_K + C^i_{K+1} = 0 \mod p, \\ C^i_{K+1} = - ( C^i_1 x_1 + C^i_2 x_2 + \dots + C^i_K x_K ) \mod p; \\ \end{array} $$
- раздаёт каждой стороне по следу в виде коэффициентов общего уравнения гиперплоскости $C^i_1, C^i_2, \dots, C^i_{K}, C^i_{K+1}$ и общему модулю $p$.
Если стороны могут собраться вместе и получить не менее чем $K$ различных гиперплоскостей, то, составив и решив систему уравнений с $K$ неизвестными, они смогут получить все координаты точки $x_1, x_2, \dots, x_k$:
Если собрано меньшее количество следов (уравнений гиперплоскостей), то их будет недостаточно для решения системы уравнений.
Пример.
Приведём пример разделения секрета по схеме Блэкли в ${{\mathbb{GF}}(11)}$. При разделении секрета $M$, используя $(3,N)$-по
Решением данной системы будет являться точка (6, 4, 2), а её первая координата – разделяемый секрет.
12.1.2. Схема разделения секрета Шамира
Схема разделения секрета Шамира (англ. Adi Shamir, [93]), также называемая схемой интерполяционных полиномов Лагранжа, основывается на том, что для восстановления всех коэффициентов полинома $P(x) = a_{K-1}x^{K-1} + \dots + a_1 x + a_0$ степени $K-1$ требуется $K$ координат различных точек, принадлежащих кривой $y=P(x)$. Все операции проводятся в конечном поле $GF(p)$.
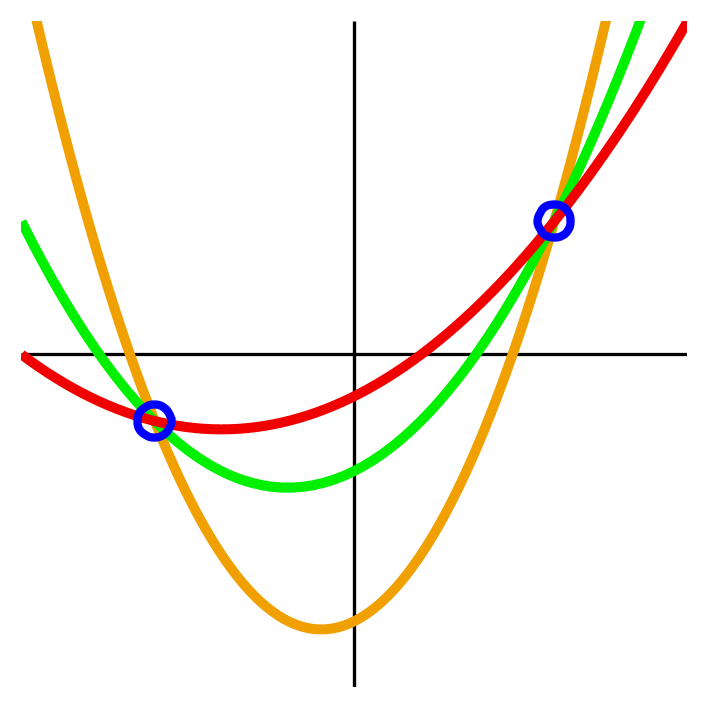
Для разделения секрета $M$ между $N$ сторонами таким образом, чтобы любые $K$ сторон могли восстановить секрет, доверенный центр выполняет следующие операции:
- выбирает несекретное большое простое число $p$ ($p > M$);
- в качестве свободного члена секретного многочлена полагает разделяемый секрет $a_0 = M$;
- выбирает остальные секретные коэффициенты многочлена $a_1, \dots, a_{k-1}$, меньшие, чем $p$;
- выбирает $N$ различных $x$, таких, что $0 < x_i < p$;
- для каждого выбранного $x_i$ вычисляет соответствующий $y_i$, подставляя значения в формулу многочлена
$$ y_i = P( x_i ) = a_{K-1}x_i^{K-1} + \dots + a_1 x_i + a_0 \mod p ;$$
- раздаёт каждой стороне по следу вида $(x_i, y_i)$ и общему модулю $p$.
Если стороны могут собраться вместе и получить не менее чем $K$ различных следов, то, составив и решив систему уравнений с $K$ неизвестными, они смогут получить все коэффициенты $a_0, a_1, \dots, a_{k-1}$ секретного многочлена:
Если собрано меньшее количество следов, то их будет недостаточно для решения системы уравнений.
Существует также способ вычисления коэффициентов многочлена, основанный на методе интерполяционных полиномов Лагранжа (откуда и берётся второе название метода разделения секрета). Идея способа состоит в вычислении набора специальных полиномов $l_i \left( x \right)$, которые принимают значение $1$ в точке $x_i$, а во всех остальных точках-следах их значение равно нулю:
Далее эти многочлены умножаются на значения $y_i$ и в сумме дают исходный многочлен:
Строго говоря, для восстановления самого секрета, которым является свободный член многочлена, не обязательно восстанавливать весь многочлен, а можно использовать упрощённую формулу для восстановления только свободного члена $a_0 = M$:
Пример. Приведём схему Шамира в поле ${{\mathbb{GF}}(p)}$. Для разделения секрета $M$ в $(3,n)$-пороговой схеме используется многочлен степени $3-1=2$.
где $p$ – простое число. Пусть $p=23$. Восстановим секрет $M$ по теням
Последовательно вычисляем
12.1.3. $(N, N)$-схема разделения секрета
Рассмотрим пороговую схему распределения одного секрета между двумя легальными пользователями. Она обозначается как $(2, 2)$-схема – это означает, что оба и только оба пользователя могут получить секрет. Предположим, что секрет $K_{0}$ – это двоичная последовательность длины $M$, $K_{0} \in {{\mathbb{Z}}}_{M}$.
Разделение секрета $K_{0}$ состоит в следующем.
- Первый пользователь в качестве секрета получает случайную двоичную последовательность $A_{1}$ длины $M$.
- Второй пользователь в качестве секрета получает случайную двоичную последовательность $A_{2} =K_{0} \oplus A_{1}$ длины $M$.
- Для получения секрета $K_{0}$ оба пользователя должны сложить по модулю 2 свои секретные ключи (последовательности) $K_{0} = A_{2} \oplus A_{1}$.
Теперь рассмотрим пороговую $(N,N)$-схему.
Имеются общий секрет $K_{0} \in {{\mathbb{Z}}}_{M}$ и $N$ легальных пользователей, которые могут получить секрет только в случае, если одновременно предъявят свои секретные ключи. Распределение секрета $K_{0}$ происходит следующим образом.
- Первый пользователь в качестве секрета получает случайную двоичную последовательность $A_{1} \in {{\mathbb{Z}}}_{M}$.
- Второй пользователь в качестве секрета получает случайную двоичную последовательность $A_{2} \in {{\mathbb{Z}}}_{M}$ и т. д.
- $(N-1)$-й пользователь в качестве секрета получает случайную двоичную последовательность $A_{N-1} \in {{\mathbb{Z}}}_{M}$.
- $N$-й пользователь в качестве секрета получает двоичную последовательность
$$ K_0 \oplus A_1 \oplus A_2 \oplus \dots \oplus A_{N-1}. $$
- Для получения секрета $K_0$ все пользователи должны сложить по модулю 2 свои последовательности:
$$ A_1 \oplus A_2 \oplus \dots \oplus A_{N-1} \oplus (K_0 \oplus A_1 \oplus A_2 \dots \oplus A_{N-1}) = K_0. $$
Предположим, что собравшихся вместе пользователей меньше общего числа $N$, например, всего $N-1$ пользователей. Тогда суммирование $N-1$ последовательностей не определяет секрета, а перебор невозможен, так как данная схема разделения секрета аналогична криптосистеме Вернама и обладает совершенной криптостойкостью.